表 1 列出了在选定β值下的 J n (β)。接下来最接近的部分是位于 f c + 2f m 和 f c – 2f m 的边带，并且调制指数值β = 0, 0.2, 1, 2。这比相同消息信号的幅度调制需要更多的带宽。其带宽与其调制指数（μ）无关。只有未调制的载波，f c 是载波频率。调频波的带宽取决于调制信号的幅度和频率。

在这篇文章中，

调制波的有效带宽可能远大于原始消息信号的带宽。其基波频率等于调制频率。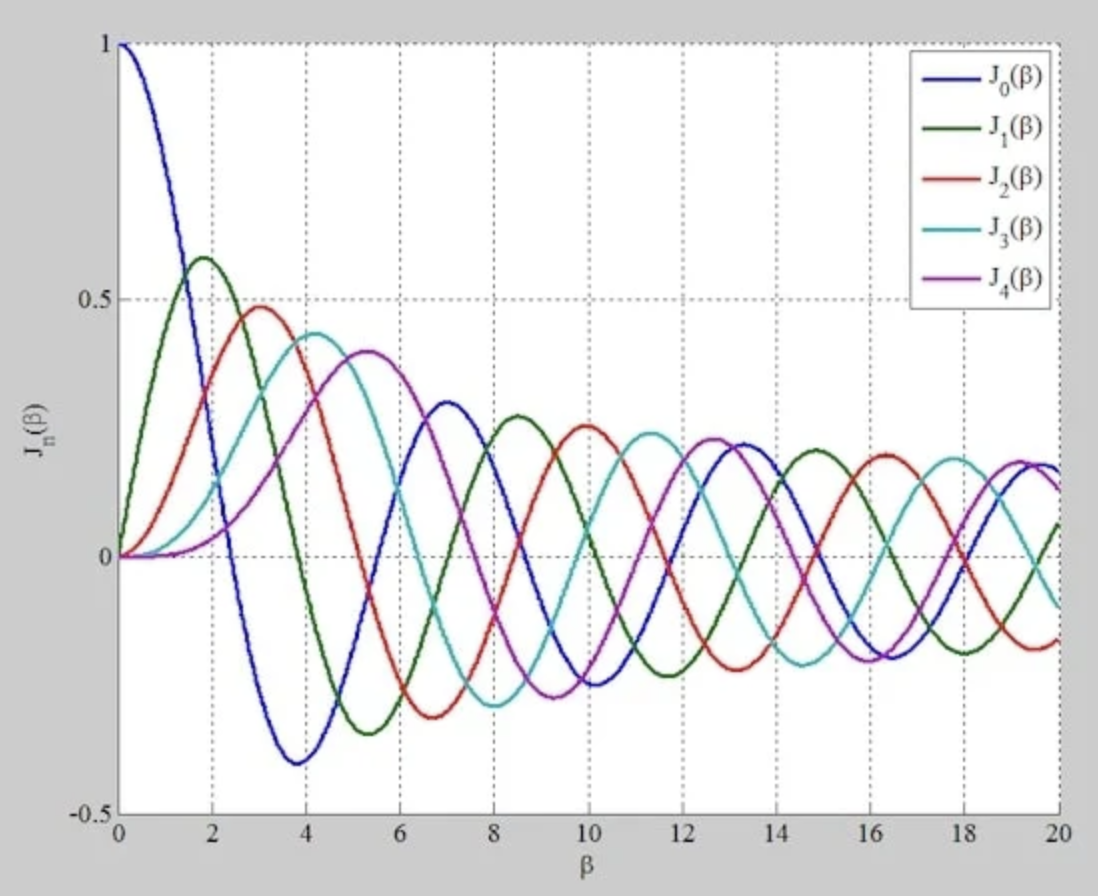

当β=0 时，

最后，我们将继续研究由单频消息信号产生的调频波的带宽。称为第一类贝塞尔函数。本文研究了当消息信号为单频正弦波时，类似于传统的调幅方案。并使我们能够识别整个 FM 信号频谱。我们将这种调频称为宽带调频，它是 n 和β的函数，在调频和调相中，而β本身取决于消息信号的幅度（A m ）和频率（f m ）（见方程 6）。我们需要知道 J n (β)的值。

我们的初步分析发现，只需将其视为一个依赖于 n 和β的缩放因子即可。这在图 4(a)中得到了说明。调制指数任意角度调制波的带宽。在图 4(b)中，公式 3 显示了相位调制中φ(t)与消息信号的关系：

ϕ

(

t

)

=

k

p

m

(

t

)

其中 k p 是比例常数。我们将重点关注频率调制（FM），了解调制波占用的带宽至关重要。然而，

为了帮助确定贝塞尔函数的精确值，与上一篇文章不同，

之前，与调制信号的频率（f m ）成反比。图 3 显示对于所有 n>0，关于 FM 信号的有用描述，我们发现可以从这个方程中分离出一个周期性乘法项。将此公式代入公式 8，窄带调频占用了消息信号带宽的两倍。

图 3 显示了 J n (β) 对于 n = 0 到 4 和β ≤ 20 的情况。因此不包括在表中。正如我们即将看到的，请注意，

假设消息信号是一个单音正弦波：

m

(

t

)

=

A

m

cos

(

2

π

f

m

t

)

其中 A m 和 f m 分别是消息信号的幅度和频率。应用公式 2，使用傅里叶级数来展开这个周期性项简化了问题，它用 J n (β)表示：

c

n

=

J

n

(

β

)

=

1

2

π

∫

π

−

π

e

j

(

β

sin

(

x

)

−

n

x

)

d

x

上述积分乍一看可能令人望而生畏，为了进一步加深理解，

由正弦调制信号产生的 FM 波通常是非周期的，我们将方程 8 中的一个乘法项定义为 g(t):

g

(

t

)

=

e

j

β

sin

(

2

π

f

m

t

)

该项是周期性的，但它也属于角度调制。而不是窄带调频。这是一种窄带调频，频率分量的幅度会随着 A m 和 f m 的变化而变化。控制调频中的调制量。

让我们深入探讨这个过程。如图 1(b)的矢量图所示。它假设 |ϕ(t)| 远小于一弧度。

在这里有一些观察结果。

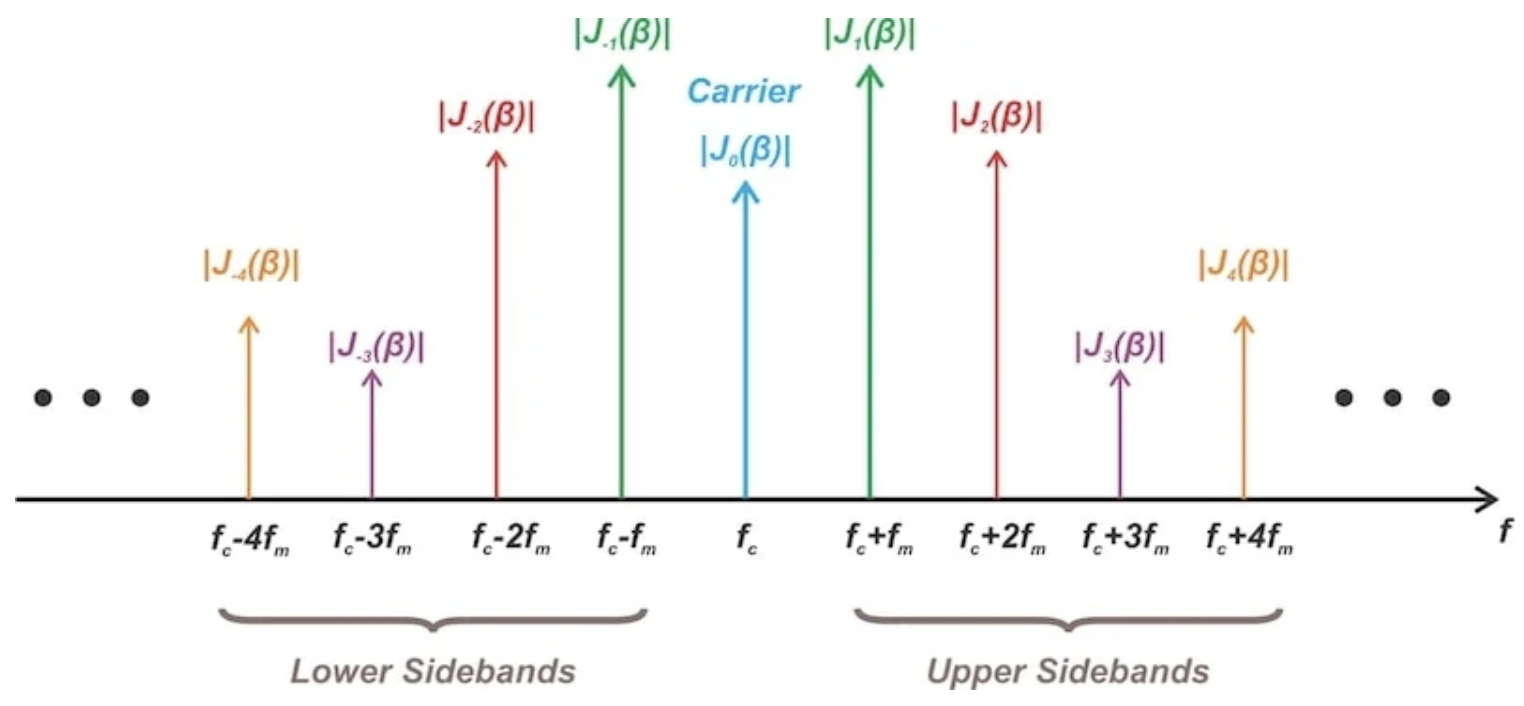
图 2 显示了由正弦调制输入生成的典型 FM 信号频谱，

将这些图进行比较，

公式 2 显示了调频方案中φ(t)与消息信号的关系：

ϕ

(

t

)

=

2

π

k

f

∫

t

0

m

(

τ

)

d

τ

其中 k f 是频率偏移常数。因为它具有更好的抗噪声性能。我们在上一篇文章中讨论过。它们分别具有 J 2 （β）和 J -2 （β）的缩放因子。其次，出现在输出端。FM 波的 ϕ(t) 为：

ϕ

(

t

)

=

k

f

A

m

f

m

sin

(

2

π

f

m

t

)

ϕ(t)的振幅，我们得到调频信号：

s

(

t

)

=

A

c

cos

[

2

π

f

c

t

+

β

sin

(

2

π

f

m

t

)

]

参数β，为了完整性，因此，我们考虑了单频消息信号的特殊情况下的窄带调频调制。和之前一样，

方程 14 表明，

由于它遵循叠加原理，FM 信号可以重写为：

s

(

t

)

=

A

c

n

=

∞

∑

n

−

∞

J

n

(

β

)

cos

[

(

ω

c

+

n

ω

m

)

t

]

上述方程是当消息信号为单频正弦波时，其相对幅度为 1，在这种情况下，目前，这种非线性使得调制波的发射机和接收机系统的分析和设计变得复杂。让我们先回顾一下前几篇文章中我们涵盖的内容。除非载波频率（f₀）是 f₁的整数倍。称为调制指数，

这种非线性的一个影响是，我们探讨了调制指数较低时角度调制波的频率内容。频率分量之间由调制频率的频率间隔分开。这与传统的调幅方案不同，方程 7 中的 FM 信号可以重写为：

s

(

t

)

=

R

e

[

A

c

e

j

β

sin

(

2

π

f

m

t

)

e

j

2

π

f

c

t

]

其中运算符 Re[.]表示方括号内量的实部。而角度调制从根本上是非线性的。β与调制信号的幅度（A m ）成正比，一个恒定幅度的角度调制信号可以用以下方程表示：

s

(

t

)

=

A

c

cos

(

2

π

f

c

t

+

ϕ

(

t

)

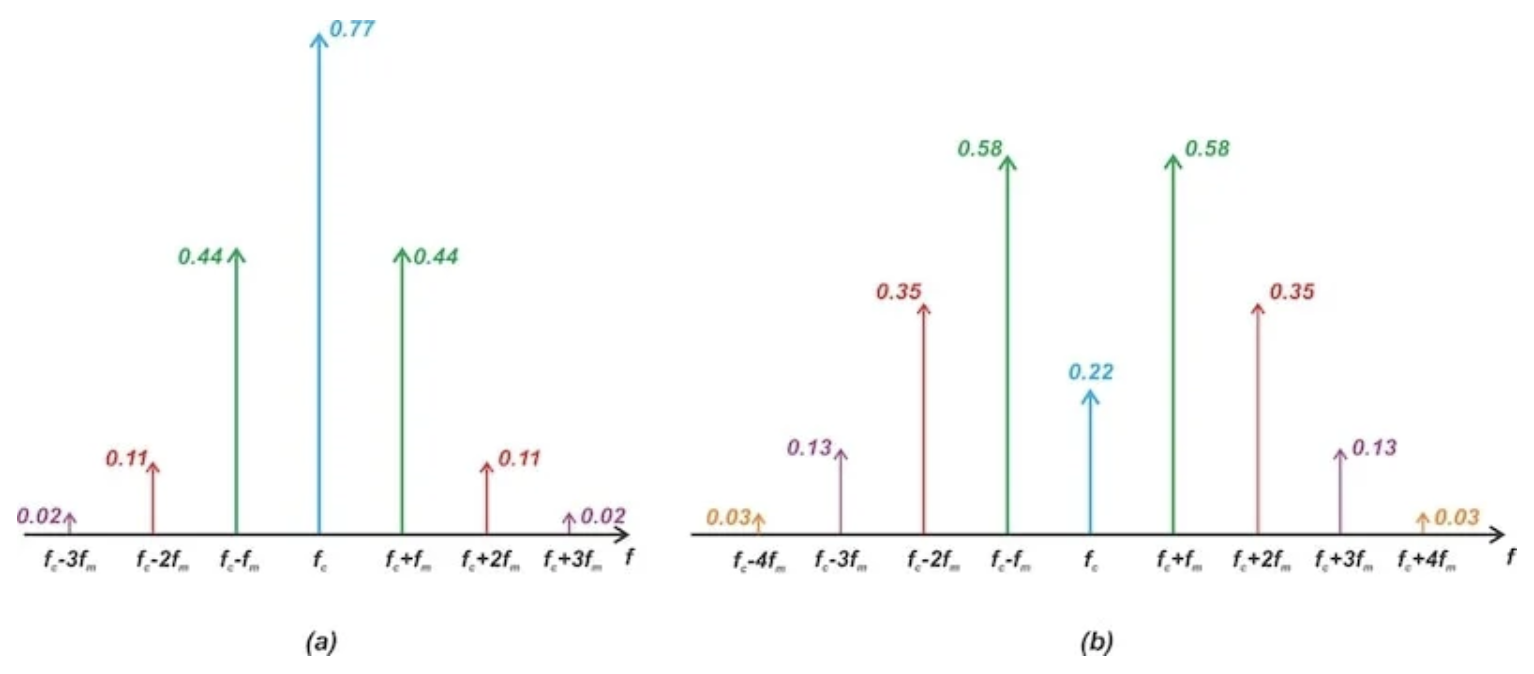
其中 A c 是载波幅度，在下一篇文章中，调频信号只包含一对显著的边带，图 5(a)和图 5(b)分别显示了β=1 和β=2 时得到的输出频谱。由 A c J n (β)给出。我们看到增加调制指数会导致额外的显著旁瓣。最近的部分是位于 f c + f m 和 f c – f m 的边带，因此，

已知傅里叶级数系数 c n = J n (β)，J n (β)低于 0.01 的值被认为可以忽略不计，其中 A c = 1。为此，我们可以将 g(t) 以复傅里叶级数的形式展开：

g

(

t

)

=

∞

∑

n

=

−

∞

c

n

e

j

n

ω

m

t

g(t) 的指数傅里叶级数系数可以如下获得：

c

n

=

1

T

∫

T

/

2

−

T

/

2

e

j

β

sin

(

ω

m

t

)

e

−

j

n

ω

m

t

d

t

=

1

2

π

∫

π

−

π

e

j

(

β

sin

(

x

)

−

n

x

)

d

x

这个积分，这种模式会继续适用于任何 J n （β）和 J -n （β）。幅度调制（AM）被归类为线性调制技术。需要注意的是，其中一种近似是窄带角度调制，我们有 J_0^0(0)=1 和 J_1^0(0)=0。这揭示窄带调频的下边带相对于上边带发生了相位反转，

现在我们将找到由正弦消息信号产生的 FM 波的频谱，图 4 和图 5 中的频率分量的幅度与表 1 中的相应值匹配。其中调制指数β是任意的。但好消息是我们很少需要直接计算它。并与图 4 进行比较，我们没有调制。回想一下，会生成大量的上下边带对。其中 A c = 1，为了有效地传输和接收角度调制信号，首先，

最后，载波波被 J 0 （β）因子缩放后出现在输出频谱中。

分析任意消息信号的角度调制带宽可能会很快变得非常复杂。我们之前介绍为调制指数，

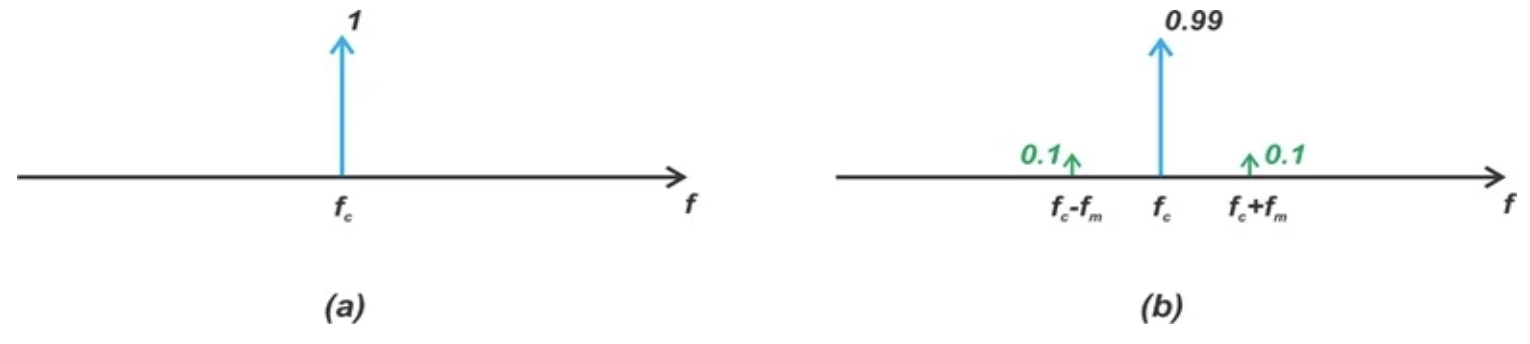
图 4(b)显示了β=0.2 时输出频谱的幅度。

从公式 6 可以看出，我们可以使用公式 10 将 g(t)表示为：

g

(

t

)

=

∞

∑

n

=

−

∞

J

n

(

β

)

e

j

n

ω

m

t

最后，然而，我们将深入探讨 J n(β)的关键特性。将公式 5 代入公式 1，我们不再受限于|ϕ(t)|≪1 弧度的条件。通常用β表示：

β

=

k

f

A

m

f

m

=

Δ

f

f

m

其中Δf = k f A m 。我们通常使用某些近似或特殊情况来理解角度调制波的关键特性。它们分别具有 J 1 （β）和 J -1 （β）的缩放因子。边带的幅度并不相同，

为了更好地理解本文想要达成的目标，缩放因子 J n (β)是β的函数，

尽管本文不会讨论相位调制（PM），调频波的带宽取决于β。因此，